Within classical physics, electrons in a conductor (or in a semiconductor) are considered as an ideal gas. Though all mobile electrons possess the charge of the same sign, they don’t push each other out of the conductor, since the classical repulsion forces are compensated by the oppositely charged ion lattice. This compensation justifies the consideration of electrons in a conductor as a weakly interacting gas. Within quantum physics, the compensation of the classical Coulomb repulsion is insufficient to describe properties of the electron system by the ideal gas model. The electron wave functions overlap, causing interelectron interactions of a quantum-mechanical origin; this is described in terms exchange and correlations. The low the system dimensionality, the more important is contribution of the electron-electron interactions. In a two-dimensional system of electrons at low densities, the potential energy of interactions may exceed the kinetic (Fermi) energy by a factor of several tens. Such interacting systems manifests properties very much different from those of the ideal electron gas газа, to the first approximation it is described in terms of the Fermi liquid theory (FL). Within the Landau FL theory, to describe properties of the interacting electron systems, novel quasiparticles are introduced (“quasielectrons”), which weakly interact with each other. The quasiparticles in the FL have the same charge and wave number as free electrons in the lattice, therefore, for simplicity, they are called “electrons”. However, other parameters of the “electrons” are very much different from those of the free electron gas.

One of the outstanding problems of modern condensed matter physics is the phase diagram and properties of strongly-interacting and disordered electron systems. The fascinating physics of strong correlations unveils when the Coulomb interaction energy exceeds the Fermi energy. The theoretical description of 2D systems has not reached a predictive stage yet, very little is known about fundamentals of strong electron-electron interactions, and about quantum ground states of disordered interacting 2D systems.
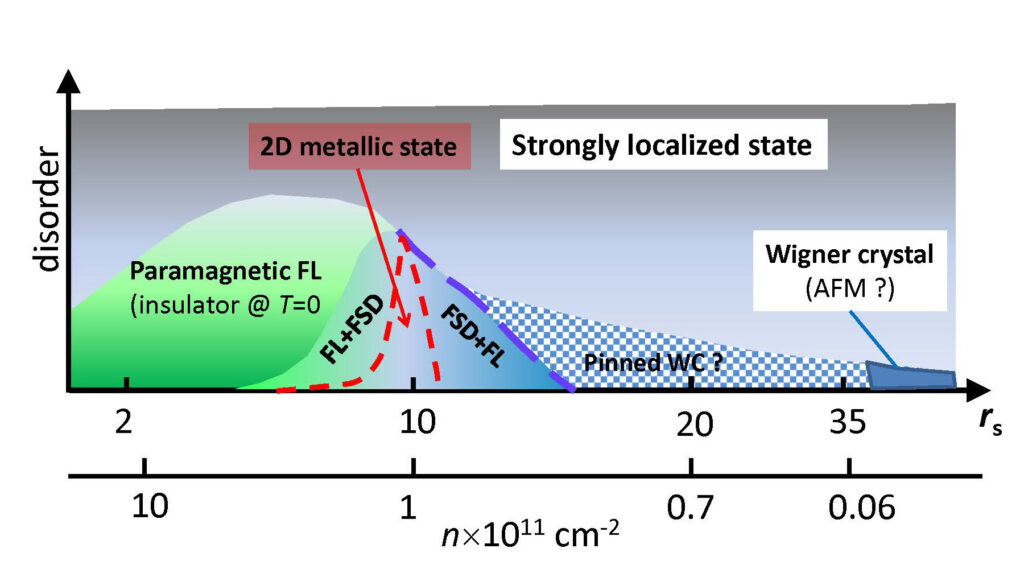
Even the ordinarytwo dimensionalelectron system exhibits nontrivial and beautiful properties, not yet fully explained within the existing theories. As interparticle interactions increase, the electron compressibility changes sign, the effective mass and g-factor Lande grow, and the spin susceptibility (Pauli) sharply raises. Therefore, the “electrons” in strongly interacting two-dimensional electron system tend to become heavier, and tend to spontaneous spin magnetization. These tendencies in the limit of strong interactions lead to the emergence of novel states of electronic matter. It is anticipated that the phase diagram of strongly interacting two-dimensional (2D) systems is remarkably rich: a multitude of electronic phases might lie between the limiting cases of a conventional paramagnetic Fermi liquid (FL) at high densities, Wigner crystal (low densities, weak disorder), and antiferromagnetic strongly localized state (strong disorder). In particular, we recently discovered spontaneous formation of ferromagnetic spin-polarized droplets (FSD), coexisting with 2D Fermi liquid. Due to interactions, the 2D system exhibits a metallic conduction, the behavior that in a sharp contrast with that for the noninteracting electron gas.
In a specially designed two-dimensional system with an equal number of electrons and holes, the particles tends to form electron-hole pairs and to condense into more energetically favorable state of the exciton insulator.

In the strongly interaction two-dimensional electron system subjected to an external quantizing magnetic field, a variety of novel phases emerge, such as Hall insulator, a state with fractionally quantized Hall resistance, reentrant transitions between the insulator and quantized Hall resistance state, composite state at half-integer filling of the Landau levels, etc. Under these conditions, the 2D system can be described as a gas of novel quasiparticles, the composite fermions consisting of electrons with flux quanta attached.
These wondering and unusual properties of strongly correlated low dimensional systems are studied in the SCES Laboratory.
